Why random rotations are good for RoPE

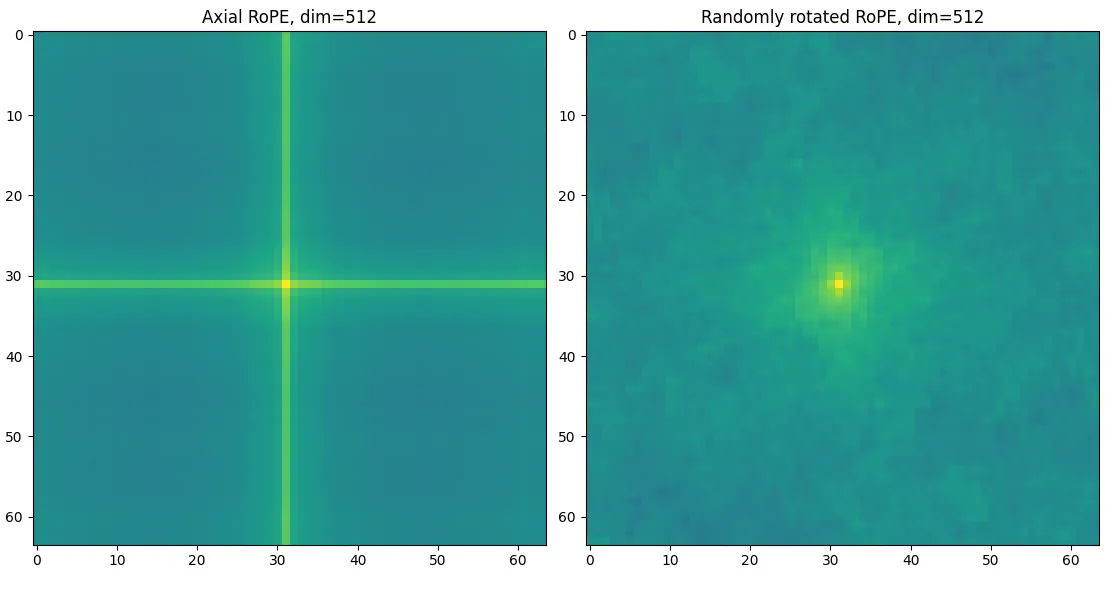
Jerry Xiong created the above picture, which started these findings. With axial RoPE (Rotary Positional Embedding), positionally attending to a single pixel causes incidental attention to a cross, because RoPE’s sine waves align. This is well-known. But he discovered that with random RoPE rotations, the cross disappears.

Random-rotation RoPE is better than your current 2D axial RoPE, and Jerry’s blog post has an even better version. Jerry’s preferred explanation is that covering angles uniformly is the goal.

However, my preferred explanation is that incoherent angles are the goal. So this blog post is an appendix, describing an optimality condition for RoPE, the math behind this RoPE variant, and where incoherence arises.

Focus on a single token

When comparing the attention operation to other architectures, the main talent of attention is its ability to attend to single keys (needle-in-a-haystack retrieval). If you disagree, then either your understanding of ML architecture is poor, or you know too much mechinterp.

Accordingly, the optimal RoPE should positionally focus on a single token. Let’s work out the math.

Notate the center of an image as complex $0+0i$, which RoPE is attending to. With $k \in {1, 2, ..., n}$ as indices, let each complex RoPE term be $c_k = e^{i \theta_k} r_k$, where $\theta_k$ is the angle and $r_k$ is the frequency’s magnitude. The attention score at a point $z$ is $\sum_k \cos(z \cdot c_k)$, where the dot is the real-plane dot product, considering the complex plane as $\mathbb R^2$.

If $S$ is the canvas, then the total positional energy of attention is its squared value, integrated over the canvas: $E = \iint_S \left(\sum_k \cos(z \cdot c_k)\right)^2 dx dy$, with $z = x + i y$. The distance-adjusted energy is $D = \iint_S \left(\sum_k \cos(z \cdot c_k) \|z\|\right)^2 dx dy$; it is the same thing multiplied by $\|z\|^2$. The ideal RoPE minimizes $D/E$, representing that attention is focused at the point $0$.

The frequencies $r_k$ are fixed, being used to control specificity and range.¹

So we can only pick the angles $\theta_k$.

At $z=0$, the attention score is $\sum_k \cos(z \cdot c_k) = \sum_k \cos(0) = n$. This represents concentrated attention. Our goal is to minimize energy away from the center, to make $D$ small. In the absence of a cancellation trick, the next best tool is to make attention behave like noise - so that different $\cos$ terms do not line up except by chance.

At points away from the center, random-rotation RoPE evaluates each channel at a position uncorrelated with other RoPE channels. The average of uncorrelated values behaves like noise, scaling as $1/\sqrt n$, while the average value at the center remains $1$. So as $n$ increases, attention can better focus on the center. Compared to axial RoPE, the stray attention on the cross doesn’t move elsewhere - it is erased.

For non-random rotations, the first guess is to set $\theta_k/\pi$ to multiples of the golden ratio. Two rotations overlapping would mean $a \varphi = b \varphi + c$ for integers $a, b, c$, leading to $c/(a-b) = \varphi$. By Hurwitz’s theorem, the golden ratio is the hardest number to approximate by rationals, so it’s good at avoiding overlaps. This produces uniform RoPE in Jerry’s blog post, where the incorrect multiple of 2 is my fault. fluffy renamed this construction Golden Gate RoPE, as it is unrelated to uniformity.

But the golden ratio neglects that our frequencies are exponentially increasing - interactions between adjacent frequencies are the strongest ones. As the separation between frequencies increases, we expect the difference between rotation angles to transition incompletely from $\pi (-1 + \sqrt 5)/2$ toward $\pi / 2$, because perpendicular angles are the most uncorrelated. And the highest and lowest frequencies will have rotations that are only surrounded on one side, not two, so they will also need special logic.

These issues are fiddly and have local minima, so let’s pretend we have infinite channels.

Suppose the frequencies are exponentially distributed as $2 \pi s^i$. Minimize the energy $E$ inside the annulus $1/s < \|z\| < 1$. This captures a slice of RoPE frequencies; the total energy away from $0$ is a concatenation of such annuluses. Truncate the frequencies to $2\pi s^{-4}, 2\pi s^{-3}, ..., 2\pi s^{3}, 2\pi s^{4}$ for numerical convenience.

Here, $D/E$ is measured when $r_k = (\text{max frequency})^{k / (\text{num frequencies} - 1)}$.

Observations

At high $s$, broad regions of angles perform comparably. This is because the higher separation between frequencies causes them to interact less.

Random rotations are not as good as chosen ones, but are better than axial RoPE. Beware that the truncation to $n$ means it’s easy to overfit. The optimal angle trends toward $\pi/2$ with higher $s$, but it’s unclear if this visualization is accurate enough to count as evidence for this effect.

The closer $s$ is to 1, the more important it is to choose a good angle.

The failure of axial RoPE (angle $0$ or $\pi/2$) is caused by having high energy in a line - which fails to decay away from the origin. This is the penalty of correlated sine waves.

In practice, I don’t expect anyone to care enough to optimize more than the single angle. $\pi (-1 + \sqrt 5)/2$ will do fine for the lazy.

Credit

Claude Code did the visualizations. To discuss this article, I’m in the EleutherAI discord. Or, qkxgecetu at mozmail dot com will work for a month.

Jerry’s blog post cites prior works such as RoPE-Mixed, but despite the similarities in final method, his discovery does not descend from them. His random-rotation picture, in which incoherence can be recognized, deserves most of the credit, a la Rosalind Franklin.

nor wrote a third post, on N-dimensional RoPE.